一、 静态链表
0、数据代替指针,描述单链表。
首先我们让数组的元素都是由两个数据域组成,data和cur。数组的每个下标都对应一个data和一个cur。data存放数据元素,游标cur相当于单链表中的next指针, 存放该元素的后继在数组中的下标。
我们把这种用数组描述的链表叫做静态链表。
//线性表的静态链表存储结构
#define MAXSIZE 1000 //假设链表的最大长度是1000
typedef struct {
ElemType data;
int cur; //游标(cur), 为0时表示无指向
}Component, StaticLinkList[MAXSIZE];我们对数组第一个和最后一个元素作为特殊元素处理,不存数据。
我们通常把未被使用的数组元素称为备用链表。
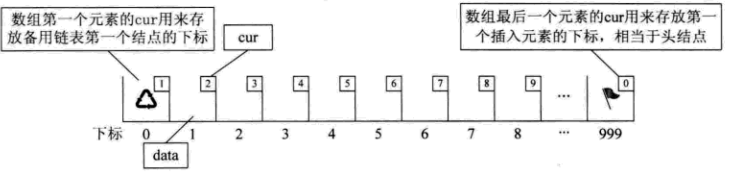
数组第一个元素,即下标为0的元素的cur存放备用链表的第一个结点的下标。
数组的最后一个元素的cur存放第一个有数组的元素的下标。
//将一维数组space中各分量链成一备用链表, space[0].cur为头指针, "0"表示空指针
Status InitList(StaticLinkList space) {
int i;
for (i=0; i<MAXSIZE-1; i++) {
space[i].cur = i+1;
}
space[MAXSIZE-1].cur = 0; //目前静态链表为空,最后一个元素的cur为0
return OK;
}假设,我们已经将数据存入静态链表,比如分别存放着“甲”, “乙”, “丁”, “戊”,“己”,“庚”等数据,则它将处理如下图所示这种状态
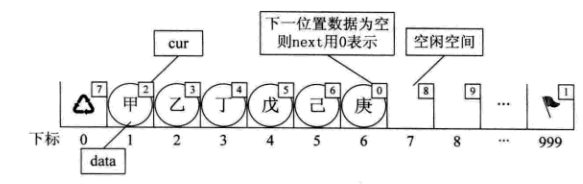
- 静态列表插入
动态链表中,结点的申请和释放分别借用malloc()和free()两个函数来实现。
静态链表中,操作的是数组,不存在结点申请和释放问题。 所以我们自己实现这两个函数。才可以做插入和删除操作。
为了辩明数组中哪些分量未被使用,解决的办法是将所有未被使用过的及已被删除的分量用游标链成一个备用的链表,每当进行插入时,便可以从备用链表上取得第一个结点作为待插入的新结点。
//若备用空间链表非空,则返回分配的结点下标,否则返回0
int Malloc_SSL(StaticLinkList space) {
int i = space[0].cur; //当前数组第一个元素的cur存的值,就是要返回的第一个备用空闲的下标
if(space[0].cur)
space[0].cur = space[i].cur; //由于要拿出一个分量来使用了,所以我们就得把它的下一个分量用来做备用
return i;
}完整代码
//在L中第i个元素之前插入新的数据元素e
Status ListInsert(StaticLinkList L, int i, ElemType e)
{
int j, k, l;
k = MAXSIZE - 1; //注意k首先是最后一个元素的下标
if (i<1 || i>ListLength(L)+1)
return ERROR;
j = Malloc_SSL(L); //获得空闲分量的下标
if(j) {
L[j].data = e; //将数据赋值给此分量的data
for(l=1; l<=i-1; i++) //找到第i个元素之前的位置
k = L[k].cur;
L[j].cur = L[k].cur; //把第i个元素之前的cur赋值给新元素的cur
L[k].cur = j; //把新元素的下标赋值给第i个元素之前元素的cur
return OK;
}
return ERROR;
}
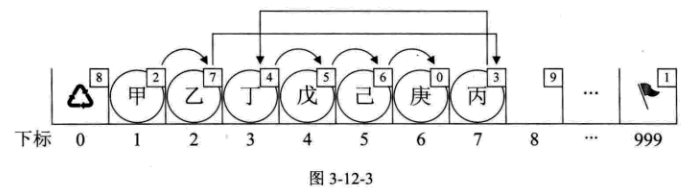
2. 静态链表的删除操作
//删除在L中第i个数据元素e
Status ListDelete(StaticLinkList L, int i) {
int j, k;
if (i<1 || i>ListLength(L))
return ERROR;
k = MAX_SIZE - 1;
for (j = 1; j<= i-1; j++)
k = L[k].cur;
j = L[k].cur;
L[k].cur = L[j].cur;
Free_SSL(L, j);
return OK;
}
void Free_SSL(StaticLinkList space, int k) {
space[k].cur = space[0].cur; //把第一个元素cur值赋给要删除的分量cur
space[0].cur = k; //把要删除的分量下标赋值给第一个元素的cur
}
int ListLength(StaticLinkList L) {
int j=0;
int i = L{MAXSIZE-1].cur;
while(i) {
i = L[i].cur;
j++;
}
return j;
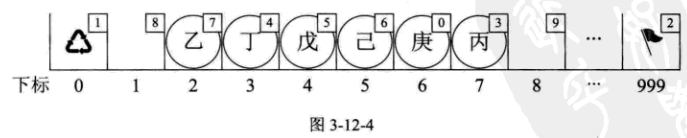
}
3. 静态链表优缺点

二、 循环链表
将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表。
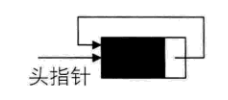

循环链表和单链表的主要差异就在于循环的判断条件上,原来判断p->next是否为空,现在则是p->next不等于头结点,则循环未结束。
单链表中,访问头结点需要O(1)的时间复杂度,尾结点则需要O(n)的时间。
有没有可能用O(1)的时间由链表指针访问到最后一个结点呢?
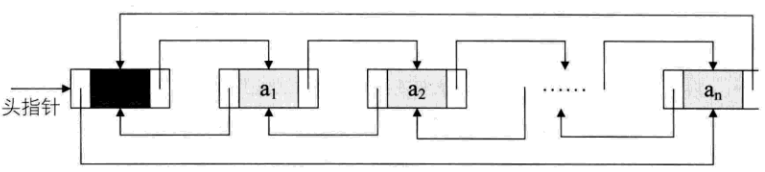
我们需要改造一下这个循环链表,不用头指针,而是用指向终端结点的尾指针来表示循环链表。

从上图中可以看到,终端结点用尾指针rear指示,则查找终端结点是O(1),而开始结点,其实就是rear->next->next,其时间复杂度也为O(1)。
举例:
将两个循环链表合并成一个表时,有了尾指针就非常简单了。
比如下面的这两个循环链表,它们的尾指针分别是rearA和rearB
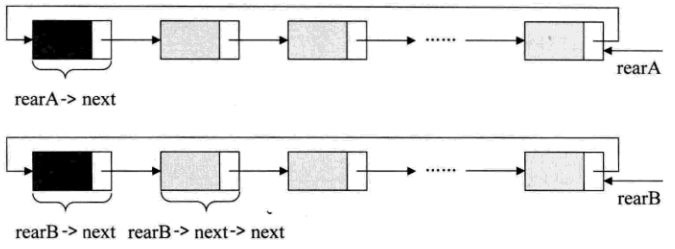
要想㧈它们合并,只需要如下的操作即可
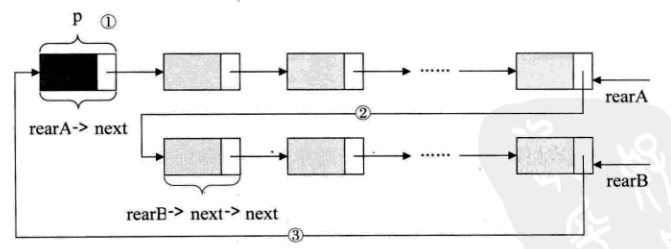
p = rearA->next; //保存A表的头结点
rearA->next = rearB->next->next; //将本是指向B表的第一个结点(不是头结点)赋值给rearA->next
rearB->next = p; //将原A表的头结点赋值给rearB->next
free(p); //释放p三、双向链表
双向链表是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。
//线性表的双向链表存储结构
typedef struct DulNode
{
ElemType data;
struct DulNode *prior; //直接前驱指针
struct DulNode *next; //直接后继指针
}DulNode, *DuLinkList;双向链表的循环带头结点的空链表
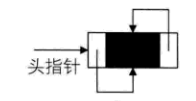
非空的循环的带头结点的双向链表
假设存储元素e的结点为s, 要实现将结点s插入到结点p和p->next之前需要下面几步。
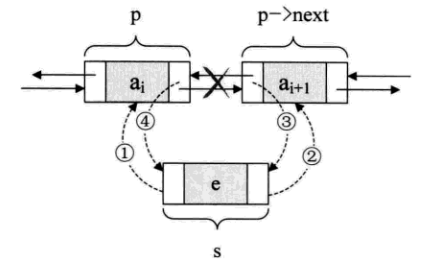
s->prior = p; //指p赋值给s的前驱,如图1
s->next = p->next; //指p->next赋值给s的后继 如图中2
p->next->prior = s; //指s赋值给p->next的前驱
p->next = s; //把s赋值给p的后继顺序:先搞定s的前驱和后继,再搞定后结点的前驱,最后解决前结点的后继。
若要删除结点p,只需要下面两步
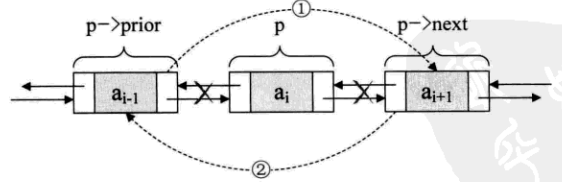
p->prior->next = p->next; //指p->next赋值给p->prior的后续
p->next->prior = p->prior; //把p->prior赋值给p->next的前驱
free(p);