1. 定义 在进行算法分析时,语句总是执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度。记作:T(n)=O(f(n))。 它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
2. 推导大O阶方法1)用常数1取代运行时间中的所有加法常数。2)在修改后的运行次数函数中,只保留最高阶项3)如果最高阶项存在且不是1,则去除与这个项相乘的常数。得到结果就是大O阶。
3. 常数阶 O(1)4. 线性阶 O(n) 循环5. 对数阶 O(logn)
int count = 1;
while(count<n) {
count = count * 2;
}由于每次count*2后,距离n更近了一分。也就是说 2^x = n 得 x = log以2为底N的对数。即时间复杂度为O(logN).
6. 平方阶 O(n^2) 循环嵌套
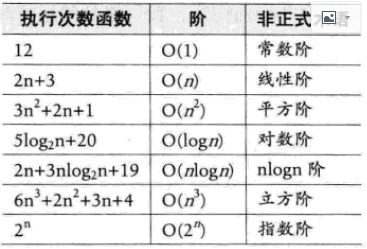
7. 常见时间复杂度